Computational Fluency: What is it?
Published: June 14, 2024
In previous blogs, we have discussed the importance of number sense. At All Learners Network (ALN) we encourage building this understanding by using number sense routines during the Launch portion of your math block. In addition to developing number sense, these routines also encourage students to work on their computational fluency. This skill is the application of students’ number sense. For example, understanding decomposing numbers into smaller, user-friendly parts, and recomposing is number sense in action toward computational fluency.
Students can apply their number sense when solving math problems with computation. In Teaching Student-Centered Mathematics: Developmentally Appropriate Instruction for Grades PreK-2, the authors discuss computational fluency as a conceptual understanding of how numbers work. With it, students gain the ability to compose, decompose, and recompose numbers in different ways. It is far more than memorizing basic facts, which are easy for students to forget when memorized over time. Computational fluency, on the other hand, allows students to have a true understanding of the values they are working with and the result they are trying to get.
CHARACTERISTICS OF COMPUTATIONAL FLUENCY
Computational fluency has three overarching characteristics. No matter what problem a student is trying to solve, whether it has basic facts or complex calculations, the characteristics of computational fluency are flexibility, efficiency, and accuracy. Let’s discuss each of these one at a time.
Flexibility
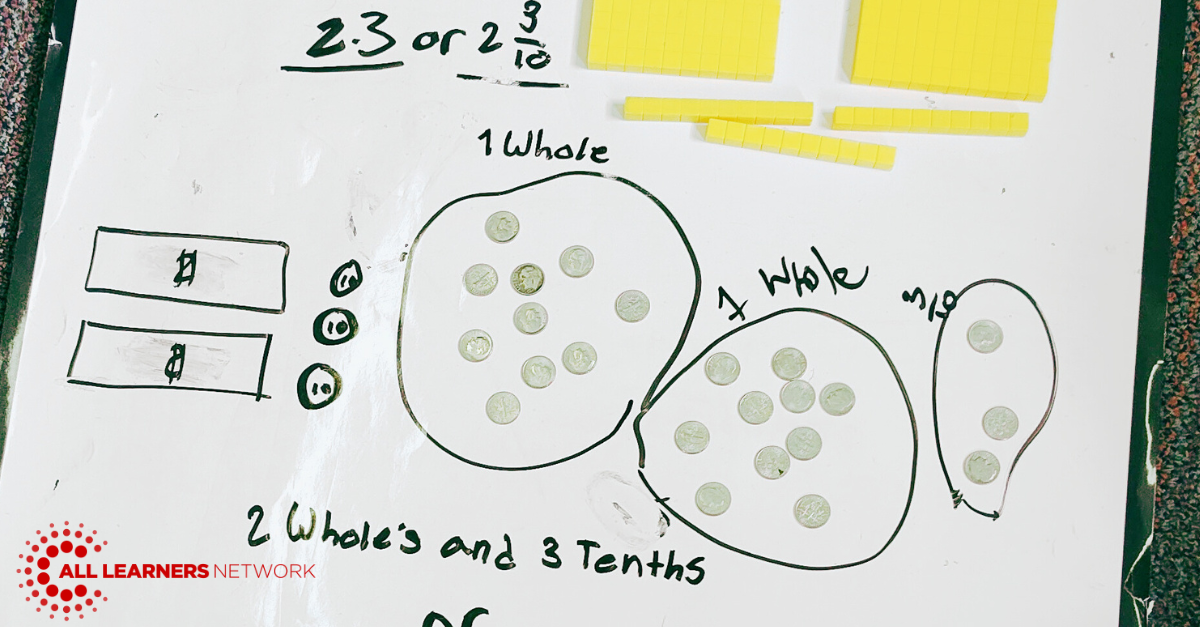
We all know that there are multiple ways to find a solution to a problem. By being flexible a student can use their understanding of number relationships with ease to solve a problem in multiple ways. Models are essential in supporting students' flexibility with different strategies. The use of models can also illuminate the similarities and differences in students’ computational strategies which can create deeper number sense as well. The practice of using Launch to highlight and discuss multiple computational strategies and models supports the development of flexibility for computational fluency.
Efficiency
Once students explore different problem-solving strategies, they can determine which strategy is the most efficient for them. As teachers, it is important to remember that efficiency is often individual. So a strategy that makes sense and is “easy” for one student will likely not be the best strategy for another. We also want to keep in mind that there is room for even greater efficiency. After students have selected a favored strategy, they should continue to discuss other strategies with their peers to see if there is an even better strategy for them to use.
Accuracy
While we do want students to be able to solve problems efficiently it is just as important that they are finding accurate and reasonable solutions. If a student has a strong number sense they should be able to determine what a reasonable answer would be before even starting calculations (for example - the answer will be a larger number… etc).
DO STANDARDIZED ALGORITHMS ALLOW FOR COMPUTATIONAL FLUENCY?
In short, no. Standardized algorithms often rely on students to memorize specific steps, which does not ensure that students have a true understanding of what the quantities mean and how the computational operations impact them. Without that understanding the student has trouble knowing if their answer is reasonable or not. (We’ve all heard a student reply to the question “Does your answer make sense?”, “That’s the way I’m supposed to do it.”)
With memorization, students spend more time thinking about where they are in the process and what comes next. Memorized algorithms are not often efficient ways for students to find solutions and they are also more likely to make mistakes. They will be more focused on the process than checking whether or not the answers they are getting are reasonable or accurate. So leaning heavily on standardized algorithms does not leave room to ensure that students are developing computational fluency.
While students develop computational fluency they should be encouraged to use their number sense. Computational Fluency can only be developed through the persistent application of students' deep understanding of number, composing and decomposing numbers through the exploration of models, and well-orchestrated discourse illuminating and comparing a variety of strategies. Given those opportunities, computational fluency is slowly and consistently built.
References
Van de Walle, J. A., Lovin, L. H., Karp, K. S., & Bay-Williams, J. M. (2018). Teaching student-centered mathematics: Developmentally appropriate instruction for grades PreK-2 (3rd ed., Vol. 1). Pearson.
Click here for the printable version.
What Now?
1. Explore the All Learners Lesson Structure.
2. Check out our blog on Exploring 4 Categories of Number Sense Routines.
3. Bring All Learners Network (ALN) into your school or district for embedded professional development.

All Learners Network is committed to a new type of math instruction. We focus on supporting pedagogy so that all students can access quality math instruction. We do this through our online platform, free resources, events, and embedded professional development. Learn more about how we work with schools and districts here.





