%20(14).png)
Why does high school math need a makeover?
There is no shortage of international studies to cast doubt on the effectiveness of American math instruction. Trends in International Mathematics and Science Study (TIMSS) and Programme for International Student Assessment (PISA) are two studies frequently referenced when discussing math disparities. These assessments warn us that the number of students who are proficient with math in the U.S. is low, especially when compared with other industrial countries like Japan, South Korea, and Finland. What’s going on?
I would argue that the lack of success in math is not a result of the competence of math teachers, the ineptitude of American curricula, or the use of technology. There may be some issues with each of these elements of instruction, but they are not the root cause of our difficulty with mathematics. American math teachers are as well prepared as teachers in most foreign countries, and as capable. American curriculums can be “a mile wide and half an inch deep” but they also address much of the same content as countries with superior math performance. The issue that keeps us from competing with others on the world stage is our pedagogy, the way we teach math. NAEP results suggest that the lowest math scores in the U.S. are at the high school level. High school pedagogy is designed, probably unintentionally, to privilege some students over others. NAEP shows that white, middle-class students are the benefactors of today’s instruction.
White, middle-class students make up the overwhelming majority of students who are math proficient. This is NOT to say that all white students are doing well in math or that the number of students of color or living in poverty aren’t some of the country's best and brightest. And- these cases are the exceptions. The number of proficient students in math in the U.S. is low. Only a quarter of high school students are math proficient, according to NAEP (and many other state assessments). This lack of proficiency has been documented for almost 50 years (See NAEP). Students living in poverty, students of color, and students with learning differences - as well as some white students - are missing out on the opportunities math can provide.
So if the teachers aren’t the issue and the students aren’t the issue, then why are American Math results so discouraging? The answer is that it is our pedagogy, the way math is taught that is so problematic. The good news is that, if we can change our approach, many more students can learn and understand math. The bad news is that this ineffective pedagogy is pervasive across the U.S. We are so used to it, so familiar with it, we tend to ignore the inequity it creates.
Current high school math instruction revolves around a principle I’ll call, "think like me." It should be familiar to everyone who has taken math in the last century. It involves a teacher showing students how to perform a mathematical operation and then students memorizing and regurgitating the teacher’s approach. While teachers believe that students will learn to understand, only a few do. Most will approximate what they think the teacher has done and others will abandon the learning completely. This is one of those instances when everyone - the teacher, the students, and the parents - believes that there is learning going on, but actually, little is happening and for only a few students. While some people would assert that students who are “naturally good at math” are the ones who are successful, there is little evidence to suggest that there is a “math gene”. There is more evidence that almost everyone can do math, that is, can reason mathematically with the concepts that occupy high school mathematics. These include solving for unknowns (simplifying expressions and equations), and understanding a wide variety of co-variation or functions. What denies the majority of students access to understanding math is that the teacher often insists on a single way of thinking about concepts and solving problems. Because of this, students who think differently than the teacher don’t have access to important concepts.
But isn’t math about knowing the right way to solve something?
We need to find answers and solve problems, but there is always more than one way to think about and do mathematics. When we streamline math into procedures and memorization, rather than exploration and understanding, we make math inaccessible to most students.
Here’s a typical type of math lesson a high school teacher might use.
The goal is to be able to get students to create a function - a kind of mathematical formula or recipe - that includes two specific points. Typically, the teacher will show students some form of the formula:
y2-y1
x2-x1
They will explain what x and y are, and how this is the slope of the line. Then they will ask students to use some points, (1,3) and (3,9) for example. The students will dutifully fill these numbers in for x and y and solve. This type of activity has a nickname, plug and chug. After being told this formula, students will get numerous examples to practice on their own. This formula is then used when teaching the formula we all know and love:
y=mx+b
Students will use the first (slope) formula to find the m and then use x and y with that m to find b. Makes sense, right? If you’re a mathematician, it will. If you’re not, it can be a little hard to follow. To be completely fair, most teachers will spend quite a bit of time explaining these formulas and giving students ways to practice them. The theory is that, by practicing, students will understand what they’re doing. Overwhelmingly, they do not.
So, how else can this be taught? I’ve been observing in an unusual high school classroom not too far from our offices. This is a class of the lowest track, meaning this local high school ability groups students based on their perceived math ability. The students in this class are perceived to have the least math acuity. Because of how they’re being taught, they usually demonstrate a greater understanding of this particular concept, the slope and equation of a linear function, than their higher-tracked classmates. The difference is the pedagogy used.
Their teacher, Ed, has focused most of the semester on the idea of the equations, points, and graphs of linear functions. Rather than move through a list of concepts to be covered, he’s focused on the most important ideas for students to understand in what could be called, “Algebra 1”. His approach was to give students very little to start with.
3 —> 9
1 —> 3
5 —> ?
He asked students to figure out “What 5 goes to”. He did not give them suggestions on how to do this. He did not ask them (at the beginning) to create tables or graphs. He simply asked what they noticed and what they wondered. Sometimes they noticed things that were relevant to where he wanted them to go, sometimes what students noticed was interesting but had nothing to do with linear functions. Students worked in groups of 2 or 3 and talked to each other and then made observations on each other’s work. Most groups had some version of this:
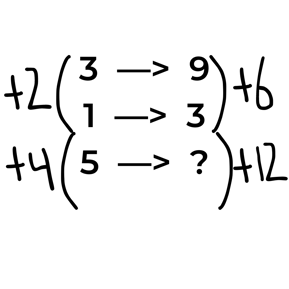
They identified the differences between starting values (x) and ending values (y). They called these “left side” and “right side” numbers. Since the values on the left doubled, they figured (correctly) that the values on the right doubled. No one told them this. They made the argument this approach allowed them to come up with a good number to use for the ?. Eventually, one of the students figured out that if you divide the difference in the right side by the difference in the left side, you can find what you multiply the left side by to get the right.
3 * 3 = 9
1 * 3 = 3
5 * 3 = 15
This discovery, which was made by students who are thought to be “not good at math” is the same concept as the formula y2-y1 / x2-x1 . What’s the big deal? Wasn’t it quicker just to tell students the formula? It was quicker, but without understanding by most students. Finding the slope with a formula is efficient but it has a black-box quality to it. Student plug and chug without understanding why what they’re doing makes sense. Or, in most cases, the only sense they can make is to repeat the teacher’s understanding. The students who constructed an understanding of slope from solving problems developed the concept from the beginning. They are able to make graphs based on their understanding of a function as a “recipe” of how one number is linked to another on a line. They are able to graph that function (or recipe) and explain why points fall on it. This is understanding that cannot be borrowed from the teacher. To be useful, mathematics has to be built in the mind of the learner. That is where understanding is made, not in the mind of the teacher.
One final note about "think like me" pedagogy: one can make that argument that it is an oppressive approach. While I know the term oppressive is loaded, I think it applies here. "Think like me" pedagogy clearly provides advantages to a particular group of people (white, middle class students). It privileges them. "Think like me" is also a pedagogy that that a teacher should tell students what to think AND how to think. Controlling student thinking and discourse seems, at least on the surface, to be oppressive to students who do not think like the teachers.
To Improve Math Instruction Teachers Should Consider:
- Teaching that encourages students to make sense of the math they do for themselves
- Encouraging students to talk with each other during class about their emerging understanding
- Listen to students' thinking to help them go deeper with understanding
Why is changing high school math important? Math is the subject with the highest correlation with graduation rates and college matriculation. If we really care that students in our country all have an opportunity to be college and career-ready, we need to change the way math is taught in high school. We need to emphasize student thinking and discourse and, as much as we can, let students do their own thinking, rather than being made to think like the teacher.
References
Liljedahl P. Zager T. & Wheeler L. (2021). Building thinking classrooms in mathematics: 14 teaching practices for enhancing learning grades k-12. Corwin. Retrieved December 18 2023 from https://us.corwin.com/books/building-thinking-classrooms-268862.
Click here for the printable version.
What Now?
-
Download and explore the All Learners Math Lesson Structure.
-
Review the Problem Introduction Protocol (PIP) and read our free book Teaching Math for All Learners.
-
Bring All Learners Network (ALN) into your school or district for embedded professional development.

All Learners Network is committed to a new type of math instruction. We focus on supporting pedagogy so that all students can access quality math instruction. We do this through our online platform, free resources, events, and embedded professional development. Learn more about how we work with schools and districts here.





